Supposons qu'un institut de sondage interroge 1 200 électeurs afin d'estimer la proportion de tous les électeurs favorables à une émission obligataire particulière. Nous nous attendrions à ce que la proportion des 1 200 électeurs du sondage qui sont en faveur soit proche de la proportion de tous les électeurs qui sont en faveur, mais cela n'est pas nécessairement vrai. Il y a un degré de hasard associé au résultat de l'enquête. S'il est fort probable que le résultat de l'enquête soit proche de la proportion réelle, nous avons confiance dans le résultat de l'enquête. S'il n'est pas particulièrement susceptible d'être proche de la proportion de la population, alors nous ne prendrions peut-être pas trop au sérieux le résultat de l'enquête. La probabilité que la proportion de l'enquête soit proche de la proportion de la population détermine notre confiance dans le résultat de l'enquête. Pour cette raison, nous aimerions pouvoir calculer cette probabilité.
3.1 Exemples d'espaces, d'événements et de leurs probabilités
OBJECTIFS D'APPRENTISSAGE
- Apprendre le concept d'espace d'échantillonnage associé à une expérience aléatoire.
- Apprendre le concept d'événement associé à une expérience aléatoire.
- Apprendre le concept de la probabilité d'un événement.
Exemples d'espaces et d'événements
Lancer un dé ordinaire à six faces est un exemple familier d' expérience aléatoire , une action pour laquelle tous les résultats possibles peuvent être répertoriés, mais pour laquelle le résultat réel d'un essai donné de l'expérience ne peut être prédit avec certitude. Dans une telle situation, nous souhaitons attribuer à chaque résultat, tel que lancer un deux, un nombre, appelé la probabilité du résultat, qui indique la probabilité que le résultat se produise. De même, nous aimerions attribuer une probabilité à tout événement ou ensemble de résultats, comme le roulement d'un nombre pair, qui indique la probabilité que l'événement se produise si l'expérience est réalisée. Cette section fournit un cadre pour discuter des problèmes de probabilité, en utilisant les termes mentionnés ci-dessus.
Définition
Une expérience aléatoire est un mécanisme qui produit un résultat défini qui ne peut être prédit avec certitude. L' espace échantillon associé à une expérience aléatoire est l'ensemble de tous les résultats possibles. Un événement est un sous-ensemble de l'espace d'échantillonnage.
Définition
Un événement E est dit se produire lors d'un essai particulier de l'expérience si le résultat observé est un élément de l'ensemble E .
EXEMPLE 1
Construire un espace échantillon pour l'expérience qui consiste à lancer une seule pièce de monnaie.
La solution:
Les résultats pourraient être étiquetés h pour pile et t pour pile. Alors l'espace d'échantillonnage est l'ensemble
EXEMPLE 2
Construire un espace échantillon pour l'expérience qui consiste à lancer un seul dé. Trouvez les événements qui correspondent aux phrases « un nombre pair est obtenu » et « un nombre supérieur à deux est obtenu ».
La solution:
Les résultats pourraient être étiquetés en fonction du nombre de points sur la face supérieure du dé. Alors l'espace d'échantillonnage est l'ensemble
Les résultats pairs sont 2, 4 et 6, donc l'événement qui correspond à la phrase "un nombre pair est lancé" est l'ensemble {2,4,6}, qu'il est naturel de désigner par la lettre E . Nous écrivons
De même, l'événement qui correspond à la phrase "un nombre supérieur à deux est lancé" est l'ensemble, que nous avons noté T .
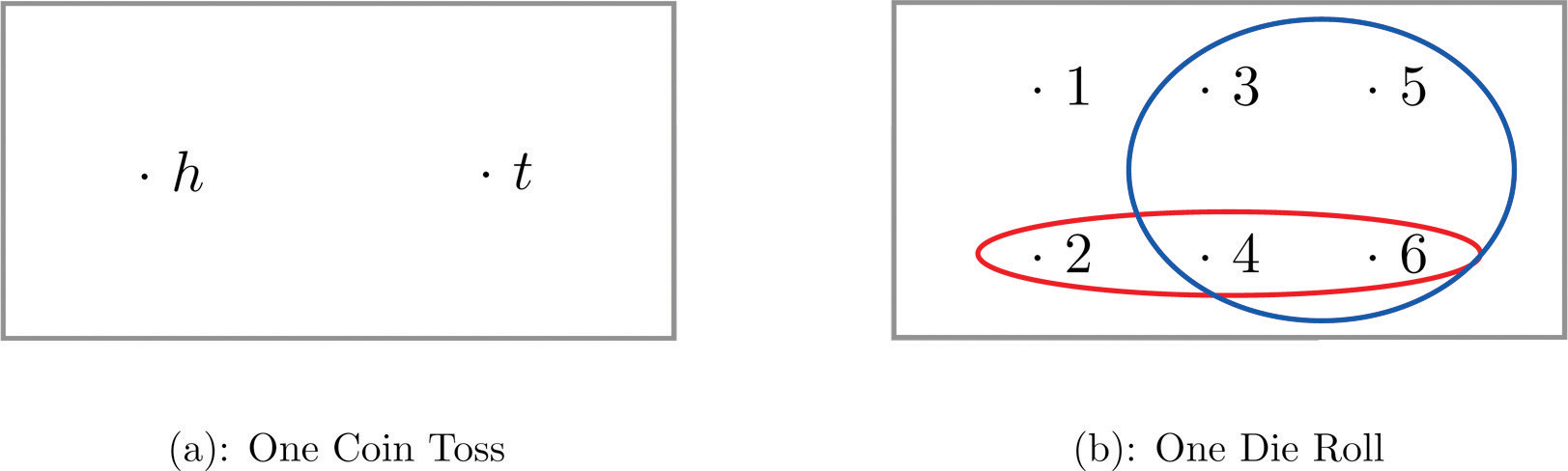
Une représentation graphique d'un espace d'échantillonnage et d'événements est un diagramme de Venn , comme illustré à la Figure 3.1 "Diagrammes de Venn pour deux espaces d'échantillonnage" pour la Note 3.6 "Exemple 1" et la Note 3.7 "Exemple 2" . En général, l'espace d'échantillonnage S est représenté par un rectangle, les résultats par des points à l'intérieur du rectangle et les événements par des ovales qui entourent les résultats qui les composent.
Figure 3.1 Diagrammes de Venn pour deux espaces échantillons
EXEMPLE 3
Une expérience aléatoire consiste à lancer deux pièces.
- Construisez un espace échantillon pour la situation où les pièces sont indiscernables, comme deux centimes neufs.
- Construire un espace d'échantillonnage pour la situation où les pièces sont distinguables, comme l'un un penny et l'autre un nickel.
La solution:
- Une fois les pièces lancées, on voit soit deux têtes, qui pourraient être étiquetées, deux queues, qui pourraient être étiquetées, ou des pièces qui diffèrent, qui pourraient être étiquetées d . Ainsi, un espace d'échantillonnage est
- Puisque nous pouvons distinguer les pièces, il y a maintenant deux façons pour les pièces de différer : les têtes de penny et les queues de nickel, ou les queues de penny et les têtes de nickel. Nous pouvons étiqueter chaque résultat sous la forme d'une paire de lettres, dont la première indique comment le sou a atterri et la seconde indique comment le nickel a atterri. Un espace échantillon est alors
Un dispositif qui peut être utile pour identifier tous les résultats possibles d'une expérience aléatoire, en particulier celle qui peut être considérée comme se déroulant par étapes, est ce qu'on appelle un diagramme en arbre . Il est décrit dans l'exemple suivant.
EXAMPLE 4
Construire un espace échantillon qui décrit toutes les familles de trois enfants selon le sexe des enfants par rapport à l'ordre de naissance.
La solution:
Deux des résultats sont "deux garçons puis une fille", que nous pourrions désigner, et « une fille puis deux garçons », que nous noteronsDe toute évidence, il existe de nombreux résultats, et lorsque nous essayons de tous les énumérer, il peut être difficile d'être sûr de les avoir tous trouvés à moins de procéder systématiquement. L'arborescence illustrée à la figure 3.2 "Arborescence pour les familles à trois enfants" , donne une approche systématique.
Illustration 3.2Diagramme en arbre pour les familles de trois enfants
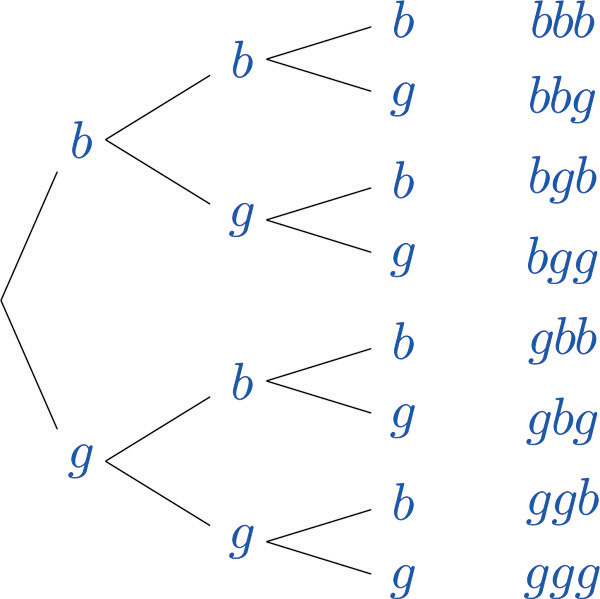
Le diagramme a été construit comme suit. Il y a deux possibilités pour le premier enfant, garçon ou fille, nous dessinons donc deux segments de ligne partant d'un point de départ, l'un se terminant par un b pour « garçon » et l'autre se terminant par un g pour « fille ». Pour chacune de ces deux possibilités pour le premier enfant, il y a deux possibilités pour le deuxième enfant, « garçon » ou « fille », donc à partir de chacun des b et g , nous dessinons deux segments de ligne, un segment se terminant par un b et un par un g . Pour chacun des quatre points de fin maintenant dans le diagramme, il y a deux possibilités pour le troisième enfant, nous répétons donc le processus une fois de plus.
Les segments de ligne sont appelés branches de l'arbre. Le point d'extrémité droit de chaque branche s'appelle un nœud . Les nœuds à l'extrême droite sont les nœuds finaux ; à chacun correspond un résultat, comme le montre la figure.
À partir de l'arbre, il est facile de lire les huit résultats de l'expérience, de sorte que l'espace d'échantillonnage est, en lisant du haut vers le bas des nœuds finaux de l'arbre,
Probabilité
Définition
La probabilité d'un résultat e dans un espace échantillon S est un nombre p compris entre 0 et 1 qui mesure la probabilité que e se produise sur un seul essai de l'expérience aléatoire correspondante. La valeur p = 0 correspond au résultat e impossible et la valeur p = 1 correspond au résultat e certain.
Définition
La probabilité d'un événement A est la somme des probabilités des résultats individuels qui le composent. Il est noté
La formule suivante exprime le contenu de la définition de la probabilité d'un événement :
Si un événement E est, alors
La figure 3.3 "Espaces d'échantillonnage et probabilité" illustre graphiquement les définitions.
Figure 3.3 Espaces d'échantillonnage et probabilité
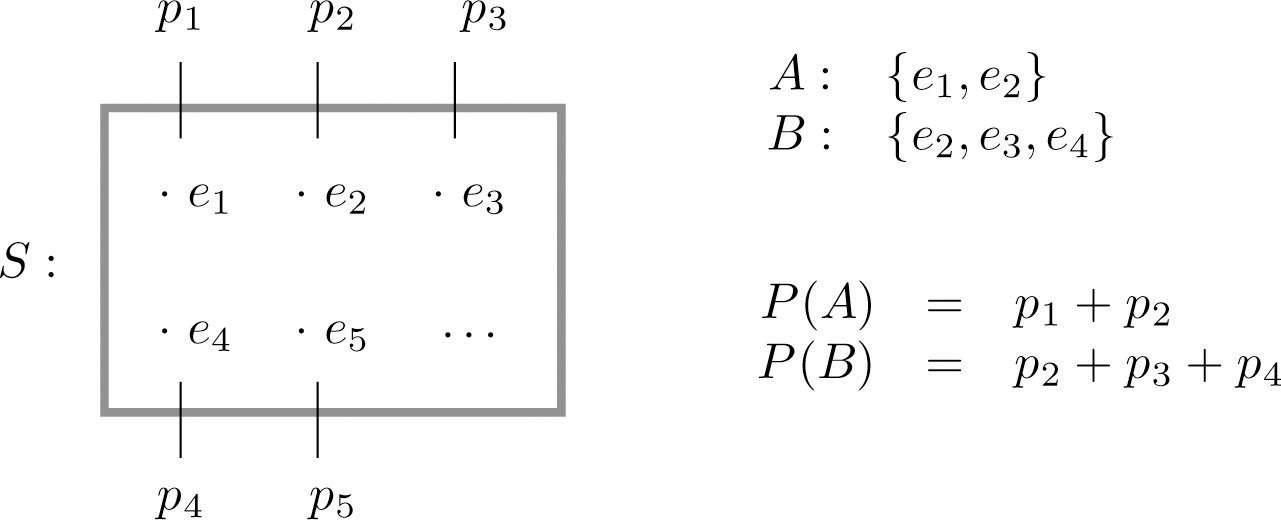
Puisque tout l'espace échantillon S est un événement qui est certain de se produire, la somme des probabilités de tous les résultats doit être le nombre 1.
Dans le langage courant, les probabilités sont souvent exprimées en pourcentages. Par exemple, nous dirions qu'il y a 70 % de chance qu'il pleuve demain, ce qui signifie que la probabilité de pluie est de 0,70. Nous utiliserons cette pratique ici, mais dans toutes les formules de calcul qui suivent nous utiliserons la forme 0,70 et non 70 %.
EXEMPLE 5
Une pièce est dite « équilibrée » ou « juste » si chaque côté est également susceptible d'atterrir. Attribuez une probabilité à chaque résultat dans l'espace de l'échantillon pour l'expérience qui consiste à lancer une seule pièce équitable.
La solution:
Avec les résultats étiquetés h pour les têtes et t pour les queues, l'espace d'échantillonnage est l'ensembleÉtant donné que les résultats ont les mêmes probabilités, qui doivent totaliser 1, chaque résultat se voit attribuer une probabilité 1/2.
EXEMPLE 6
Un dé est dit "équilibré" ou "juste" si chaque face a la même probabilité d'atterrir sur le dessus. Attribuez une probabilité à chaque résultat dans l'espace de l'échantillon pour l'expérience qui consiste à lancer un seul dé équitable. Trouvez les probabilités des événements E : « un nombre pair sort » et T : « un nombre supérieur à deux sort ».
La solution:
Avec les résultats étiquetés en fonction du nombre de points sur la face supérieure du dé, l'espace échantillon est l'ensemblePuisqu'il y a six résultats également probables, qui doivent totaliser 1, chacun se voit attribuer une probabilité de 1/6.
Depuis,
Depuis,
EXEMPLE 7
Deux pièces équitables sont lancées. Trouvez la probabilité que les pièces correspondent, c'est-à-dire, soit les deux faces terrestres, soit les deux faces terrestres.
La solution:
Dans la note 3.8 "Exemple 3" , nous avons construit l'espace d'échantillonnagepour la situation dans laquelle les pièces sont identiques et l'espace échantillonpour la situation dans laquelle les deux pièces peuvent être distinguées.
La théorie des probabilités ne nous dit pas comment attribuer des probabilités aux résultats, mais seulement ce qu'il faut en faire une fois qu'ils sont attribués. Plus précisément, en utilisant l'espace d'échantillonnage S , la correspondance des pièces est l'événement, qui a une probabilitéUtilisation de l'espace échantillon, l'appariement des pièces est l'événement, qui a une probabilitéDans le monde physique, cela ne devrait faire aucune différence que les pièces soient identiques ou non, et nous aimerions donc attribuer des probabilités aux résultats afin que les nombresetsont les mêmes et correspondent le mieux à ce que nous observons lorsque des expériences physiques réelles sont effectuées avec des pièces qui semblent justes. L'expérience réelle suggère que les résultats danssont également probables, nous attribuons donc à chaque probabilité 1∕4, puis
De même, d'après l'expérience, les choix appropriés pour les résultats dans S sont :
qui donnent la même réponse finale
Les trois exemples précédents illustrent comment les probabilités peuvent être calculées simplement en comptant lorsque l'espace d'échantillonnage se compose d'un nombre fini de résultats également probables. Dans certaines situations, les résultats individuels de tout espace échantillon qui représente l'expérience sont inévitablement inégalement probables, auquel cas les probabilités ne peuvent pas être calculées simplement en comptant, mais la formule de calcul donnée dans la définition de la probabilité d'un événement doit être utilisée.
EXEMPLE 8
La répartition du corps étudiant dans un lycée local selon la race et l'origine ethnique est de 51% de blancs, 27% de noirs, 11% d'hispaniques, 6% d'asiatiques et 5% pour tous les autres. Un élève est tiré au sort dans ce lycée. (Sélectionner "au hasard" signifie que chaque élève a la même chance d'être sélectionné.) Trouvez les probabilités des événements suivants :
- B : l'élève est noir,
- M : l'élève est minoritaire (c'est-à-dire pas blanc),
- N : l'élève n'est pas noir.
La solution:
L'expérience est l'action de sélectionner au hasard un élève parmi la population étudiante du lycée. Un espace échantillon évident estÉtant donné que 51 % des étudiants sont blancs et que tous les étudiants ont la même chance d'être sélectionnés,, et de même pour les autres résultats. Ces informations sont résumées dans le tableau suivant :
- Depuis,
- Depuis,
- Depuis,
EXEMPLE 9
La population étudiante du lycée considérée dans la note 3.18 "Exemple 8" peut être répartie en dix catégories comme suit : 25 % d'hommes blancs, 26 % de femmes blanches, 12 % d'hommes noirs, 15 % de femmes noires, 6 % d'hommes hispaniques, 5 % de femmes hispaniques, 3 % d'hommes asiatiques, 3 % de femmes asiatiques, 1 % d'hommes d'autres minorités combinées et 4 % de femmes d'autres minorités combinées. Un élève est tiré au sort dans ce lycée. Trouvez les probabilités des événements suivants :
- B : l'élève est noir,
- : l'élève est une femme minoritaire,
- : l'étudiant est une femme et n'est pas noir.
La solution:
Maintenant, l'espace d'échantillonnage estLes informations données dans l'exemple peuvent être résumées dans le tableau suivant, appelé tableau de contingence à double entrée :
| Le genre | Race / Origine ethnique | ||||
|---|---|---|---|---|---|
| Blanc | Le noir | hispanique | asiatique | Les autres | |
| Homme | 0,25 | 0,12 | 0,06 | 0,03 | 0,01 |
| Femelle | 0,26 | 0,15 | 0,05 | 0,03 | 0,04 |
- Depuis,
- Depuis,
- Depuis,
POINTS CLÉS À RETENIR
- L'espace d'échantillonnage d'une expérience aléatoire est la collection de tous les résultats possibles.
- Un événement associé à une expérience aléatoire est un sous-ensemble de l'espace échantillon.
- La probabilité de tout résultat est un nombre compris entre 0 et 1. Les probabilités de tous les résultats totalisent 1.
- La probabilité de tout événement A est la somme des probabilités des résultats dans A .
DES EXERCICES
Une boîte contient 10 billes blanches et 10 billes noires. Construisez un espace échantillon pour l'expérience consistant à tirer au hasard, avec remplacement, deux billes successivement et à noter la couleur à chaque fois. (Piocher « avec remise » signifie que la première bille est remise en place avant que la deuxième bille ne soit tirée.)
Une boîte contient 16 billes blanches et 16 billes noires. Construisez un espace échantillon pour l'expérience consistant à tirer au hasard, avec remplacement, trois billes successivement et à noter la couleur à chaque fois. (Piocher « avec remplacement » signifie que chaque bille est remise en place avant que la bille suivante ne soit tirée.)
Une boîte contient 8 billes rouges, 8 jaunes et 8 vertes. Construisez un espace échantillon pour l'expérience consistant à tirer au hasard, avec remplacement, deux billes successivement et à noter la couleur à chaque fois.
A box contains 6 red, 6 yellow, and 6 green marbles. Construct a sample space for the experiment of randomly drawing out, with replacement, three marbles in succession and noting the color each time.
Dans la situation de l'exercice 1, énumérez les résultats qui comprennent chacun des événements suivants.
- Au moins une bille de chaque couleur est tirée.
- Aucune bille blanche n'est dessinée.
Dans la situation de l'exercice 2, énumérez les résultats qui comprennent chacun des événements suivants.
- Au moins une bille de chaque couleur est tirée.
- Aucune bille blanche n'est dessinée.
- Plus de billes noires que blanches sont dessinées.
Dans la situation de l'exercice 3, énumérez les résultats qui comprennent chacun des événements suivants.
- Aucune bille jaune n'est dessinée.
- Les deux billes dessinées ont la même couleur.
- Au moins une bille de chaque couleur est tirée.
Dans la situation de l'exercice 4, énumérez les résultats qui comprennent chacun des événements suivants.
- Aucune bille jaune n'est dessinée.
- Les trois billes tirées ont la même couleur.
- Au moins une bille de chaque couleur est tirée.
En supposant que chaque résultat est également probable, trouvez la probabilité de chaque événement dans l'exercice 5.
En supposant que chaque résultat est également probable, trouvez la probabilité de chaque événement dans l'exercice 6.
En supposant que chaque résultat est également probable, trouvez la probabilité de chaque événement dans l'exercice 7.
En supposant que chaque résultat est également probable, trouvez la probabilité de chaque événement dans l'exercice 8.
Un espace échantillon estIdentifier deux événements commeetSupposeretsont chacun 0,2 etetsont chacun 0,1.
- Déterminez cedoit être.
- Trouver
- Trouver
Un espace échantillon estIdentifier deux événements commeetSupposer,, et
- Déterminez cedoit être.
- Trouver
- Trouver
Un espace échantillon estIdentifier deux événements commeetLes probabilités de certains des résultats sont données par le tableau suivant :
- Déterminez cedoit être.
- Trouver
- Trouver
Un espace échantillon estIdentifier deux événements commeetLes probabilités de certains des résultats sont données par le tableau suivant :
- Déterminez cedoit être.
- Trouver
- Trouver
DE BASE
L'espace d'échantillonnage qui décrit toutes les familles de trois enfants selon le sexe des enfants par rapport au rang de naissance a été construit à la note 3.9 "Exemple 4" . Identifiez les résultats qui comprennent chacun des événements suivants dans l'expérience de sélection aléatoire d'une famille de trois enfants.
- Au moins un enfant est une fille.
- Au plus un enfant est une fille.
- Tous les enfants sont des filles.
- Exactement deux des enfants sont des filles.
- Le premier né est une fille.
L'espace d'échantillonnage qui décrit trois lancers de pièce est le même que celui construit dans la note 3.9 "Exemple 4" avec "garçon" remplacé par "face" et "fille" remplacé par "face". Identifiez les résultats qui comprennent chacun des événements suivants dans l'expérience de lancer une pièce trois fois.
- La pièce atterrit face plus souvent que pile.
- La pièce atterrit face le même nombre de fois qu'elle atterrit pile.
- La pièce atterrit face au moins deux fois.
- La pièce tombe face au dernier lancer.
En supposant que les résultats sont également probables, trouvez la probabilité de chaque événement dans l'exercice 17.
En supposant que les résultats sont également probables, trouvez la probabilité de chaque événement dans l'exercice 18.
APPLICATIONS
Le tableau de contingence à double entrée suivant donne la répartition de la population dans un lieu particulier en fonction de l'âge et de la consommation de tabac :
Âge Tabagisme Fumeur Non fumeur Moins de 30 ans 0,05 0,20 Plus de 30 0,20 0,55 Une personne est choisie au hasard. Trouvez la probabilité de chacun des événements suivants.
- La personne est fumeuse.
- La personne a moins de 30 ans.
- La personne est un fumeur de moins de 30 ans.
Le tableau de contingence à double entrée suivant donne la répartition de la population dans un lieu particulier en fonction de l'appartenance à un parti ( A , B , C ou None ) et de l'opinion sur une émission obligataire :
Affiliation Opinion Faveurs S'oppose Indécis UN 0,12 0,09 0,07 B 0,16 0,12 0,14 C 0,04 0,03 0,06 Aucun 0,08 0,06 0,03 Une personne est choisie au hasard. Trouvez la probabilité de chacun des événements suivants.
- La personne est affiliée à la partie B .
- La personne est affiliée à un parti.
- La personne est favorable à l'émission obligataire.
- La personne n'a aucune affiliation à un parti et est indécise quant à l'émission d'obligations.
Le tableau de contingence à double entrée suivant donne la répartition de la population des femmes mariées ou précédemment mariées au-delà de l'âge de procréer dans une localité donnée selon l'âge au premier mariage et le nombre d'enfants :
Âge Nombre d'enfants 0 1 ou 2 3 ou plus Moins de 20 ans 0,02 0,14 0,08 20–29 0,07 0,37 0,11 30 ans et plus 0,10 0,10 0,01 Une femme est choisie au hasard. Trouvez la probabilité de chacun des événements suivants.
- La femme était dans la vingtaine lors de son premier mariage.
- La femme avait 20 ans ou plus lors de son premier mariage.
- La femme n'avait pas d'enfant.
- La femme était dans la vingtaine lors de son premier mariage et avait au moins trois enfants.
Le tableau de contingence à double entrée suivant donne la répartition de la population d'adultes dans un lieu particulier selon le niveau d'éducation le plus élevé et selon que l'individu prend régulièrement ou non des compléments alimentaires :
Éducation Utilisation de suppléments Prend Ça ne prend pas Pas de diplôme d'études secondaires 0,04 0,06 Baccalauréat 0,06 0,44 Diplôme de premier cycle 0,09 0,28 Diplôme d'études supérieures 0,01 0,02 Un adulte est choisi au hasard. Trouvez la probabilité de chacun des événements suivants.
- La personne a un diplôme d'études secondaires et prend régulièrement des compléments alimentaires.
- La personne a un diplôme de premier cycle et prend régulièrement des compléments alimentaires.
- La personne prend régulièrement des compléments alimentaires.
- La personne ne prend pas régulièrement de compléments alimentaires.
EXERCICES SUPPLÉMENTAIRES
Les grands ensembles de données 4 et 4A enregistrent les résultats de 500 lancers de pièces. Trouvez la fréquence relative de chaque résultat 1, 2, 3, 4, 5 et 6. La pièce semble-t-elle « équilibrée » ou « juste » ?
Les grands ensembles de données 6, 6A et 6B enregistrent les résultats d'une enquête aléatoire auprès de 200 électeurs dans chacune des deux régions, dans laquelle on leur a demandé d'exprimer s'ils préféraient le candidat A pour un siège au Sénat américain ou s'ils préféraient un autre candidat.
- Trouvez la probabilité qu'un électeur choisi au hasard parmi ces 400 préfère le candidat A .
- Trouvez la probabilité qu'un électeur sélectionné au hasard parmi les 200 qui vivent dans la région 1 préfère le candidat A (enregistré séparément dans le grand ensemble de données 6A).
- Trouvez la probabilité qu'un électeur sélectionné au hasard parmi les 200 qui vivent dans la région 2 préfère le candidat A (enregistré séparément dans le grand ensemble de données 6B).
EXERCICES SUR DE GRANDS ENSEMBLES DE DONNÉES
Remarque : Ces ensembles de données sont manquants, mais les questions sont fournies ici à titre de référence.
RÉPONSES
- ∅
- 2/4
- 1/4
- 4/9
- 3/9
- 0
- 0,4
- 0,5
- 0,4
- 0,21
- 0,6
- 0,61
- 7/8
- 4/8
- 1/8
- 3/8
- 4/8
- 0,25
- 0,25
- 0,05
- 0,55
- 0,76
- 0,19
- 0,11
Les fréquences relatives de 1 à 6 sont 0,16, 0,194, 0,162, 0,164, 0,154 et 0,166. Il semblerait que le dé ne soit pas équilibré.
3.2 Compléments, intersections et unions
OBJECTIFS D'APPRENTISSAGE
- Apprendre comment certains événements sont naturellement exprimables en termes d'autres événements.
- Apprendre à utiliser des formules spéciales pour la probabilité d'un événement exprimée en termes d'un ou de plusieurs autres événements.
Certains événements peuvent être naturellement exprimés en termes d'autres événements, parfois plus simples.
Compléments
Définition
Le complément d'un événement A dans un espace échantillon S , noté A c , est la collection de tous les résultats dans S qui ne sont pas des éléments de l'ensemble A . Cela correspond à nier toute description verbale de l'événement A .
EXEMPLE 10
Deux événements liés à l'expérience de lancer un seul dé sont E : « le nombre obtenu est pair » et T : « le nombre obtenu est supérieur à deux ». Trouvez le complément de chacun.
La solution:
Dans l'espace échantillonles ensembles de résultats correspondants sontetLes compléments sontet
En mots, les compléments sont décrits par "le nombre obtenu n'est pas pair" et "le nombre obtenu n'est pas supérieur à deux". Bien sûr, des descriptions plus faciles seraient "le nombre obtenu est impair" et "le nombre obtenu est inférieur à trois".
S'il y a 60 % de chances qu'il pleuve demain, quelle est la probabilité qu'il fasse beau ? La réponse évidente, 40 %, est un exemple de la règle générale suivante.
Règle de probabilité pour les compléments
Cette formule est particulièrement utile lorsqu'il est difficile de déterminer directement la probabilité d'un événement.
EXEMPLE 11
Trouvez la probabilité qu'au moins un face apparaisse dans cinq lancers d'une pièce équitable.
La solution:
Identifier les résultats par des listes de cinq h s et t s, commeetBien qu'il soit fastidieux de tous les énumérer, il n'est pas difficile de les dénombrer. Pensez à utiliser un diagramme en arbre pour le faire. Il y a deux choix pour le premier lancer. Pour chacun d'entre eux, il y a deux choix pour le deuxième lancer, d'oùrésultats pour deux lancers. Pour chacun de ces quatre résultats, il y a deux possibilités pour le troisième lancer, doncrésultats pour trois lancers. De même, il y arésultats pour quatre lancers et enfinrésultats pour cinq lancers.
Soit O l'événement « au moins une face ». Il existe de nombreuses façons d'obtenir au moins un face, mais une seule pour ne pas y parvenir : tout pile. Ainsi bien qu'il soit difficile de lister tous les résultats qui forment O , il est facile d'écrirePuisqu'il y a 32 résultats également probables, chacun a une probabilité de 1/32, donc, Par conséquentsoit environ 97 % de chances.
Intersection d'événements
Définition
L' intersection des événements A et B , notée A ∩ B , est la collection de tous les résultats qui sont des éléments des deux ensembles A et B . Cela correspond à combiner les descriptions des deux événements en utilisant le mot « et ».
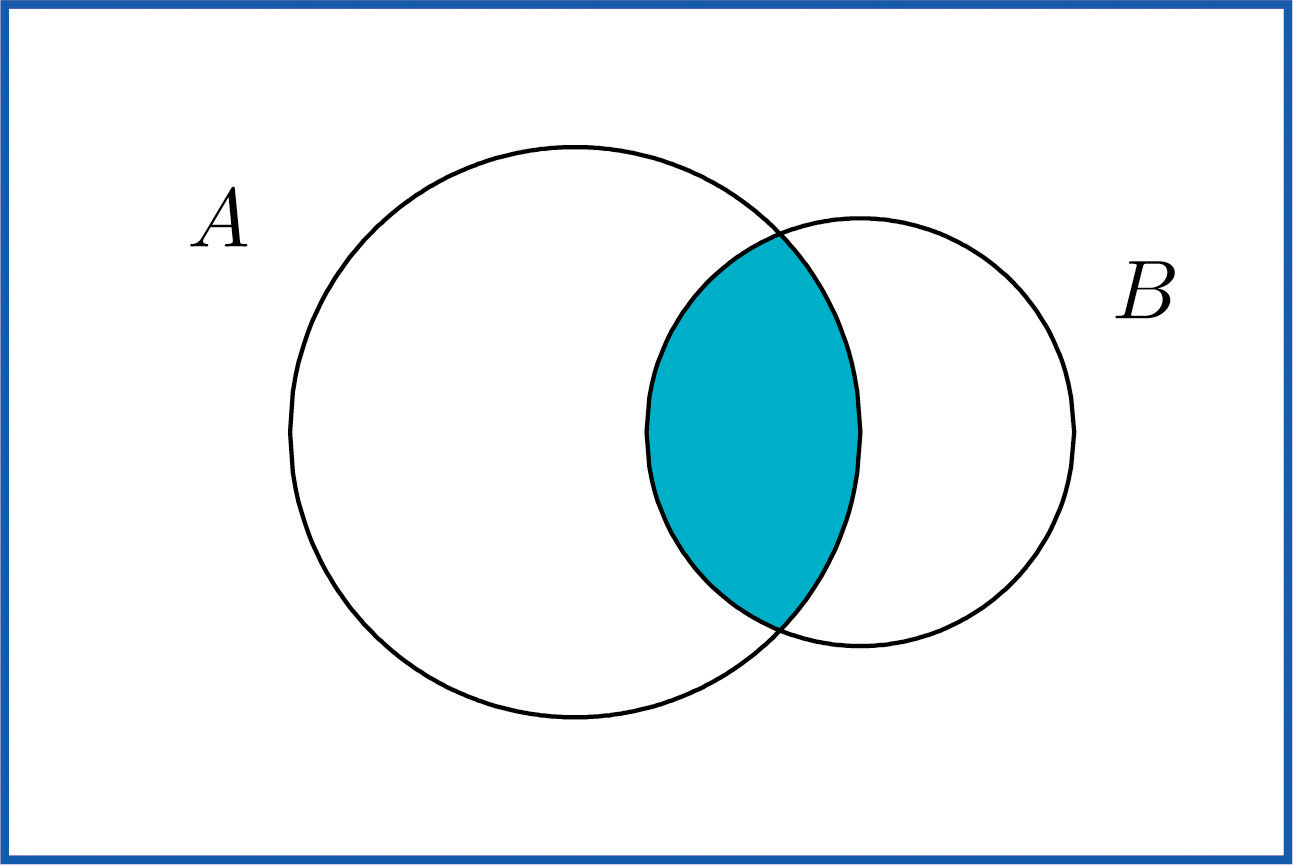
Dire que l'événement A ∩ B s'est produit signifie que lors d'un essai particulier de l'expérience, A et B se sont produits. Une représentation visuelle de l'intersection des événements A et B dans un espace échantillon S est donnée dans la Figure 3.4 "L'intersection des événements" . L'intersection correspond à la région ombrée en forme de lentille qui se trouve dans les deux ovales.
Figure 3.4 L'intersection des événements A et B
EXEMPLE 12
Dans l'expérience du lancer d'un seul dé, trouvez l'intersection E ∩ T des événements E : « le nombre obtenu est pair » et T : « le nombre obtenu est supérieur à deux ».
La solution:
L'espace échantillon estÉtant donné que les résultats qui sont communs àetsont 4 et 6,
En mots, l'intersection est décrite par "le nombre obtenu est pair et supérieur à deux". Les seuls nombres entre un et six qui sont à la fois pairs et supérieurs à deux sont quatre et six, correspondant à E ∩ T donné ci-dessus.
EXEMPLE 13
Un seul dé est lancé.
- Supposons que le dé soit juste. Trouvez la probabilité que le nombre obtenu soit à la fois pair et supérieur à deux.
- Supposons que le dé ait été "chargé" de sorte que,, et les quatre résultats restants sont également probables les uns avec les autres. Trouvez maintenant la probabilité que le nombre obtenu soit à la fois pair et supérieur à deux.
La solution:
Dans les deux cas, l'espace d'échantillonnage estet l'événement en question est l'intersectionde l'exemple précédent.
- Puisque le dé est juste, tous les résultats sont également probables, donc en comptant nous avons
Les informations sur les probabilités des six résultats que nous avons jusqu'à présent sont
Depuiset les probabilités des six résultats totalisent 1,
Ainsi, alorsEn particulierPar conséquent
Définition
Les événements A et B sont mutuellement exclusifs s'ils n'ont aucun élément en commun.
Pour A et B , n'avoir aucun résultat en commun signifie précisément qu'il est impossible que A et B se produisent tous les deux lors d'un seul essai de l'expérience aléatoire. Cela donne la règle suivante.
Règle de probabilité pour les événements mutuellement exclusifs
Les événements A et B s'excluent mutuellement si et seulement si
Tout événement A et son complément A c sont mutuellement exclusifs, mais A et B peuvent être mutuellement exclusifs sans être complémentaires.
EXEMPLE 14
Dans l'expérience du lancer d'un seul dé, trouvez trois choix pour un événement A afin que les événements A et E : "le nombre obtenu est pair" s'excluent mutuellement.
La solution:
Depuiset nous voulons que A n'ait aucun élément en commun avec E , tout événement qui ne contient aucun nombre pair fera l'affaire. Trois choix sont {1,3,5} (le complément E c , les cotes), {1,3} et {5}.
Union des événements
Définition
L' union des événements A et B , notée A ∪ B , est la collection de tous les résultats qui sont des éléments de l'un ou l'autre des ensembles A et B , ou des deux. Cela correspond à combiner les descriptions des deux événements en utilisant le mot « ou ».
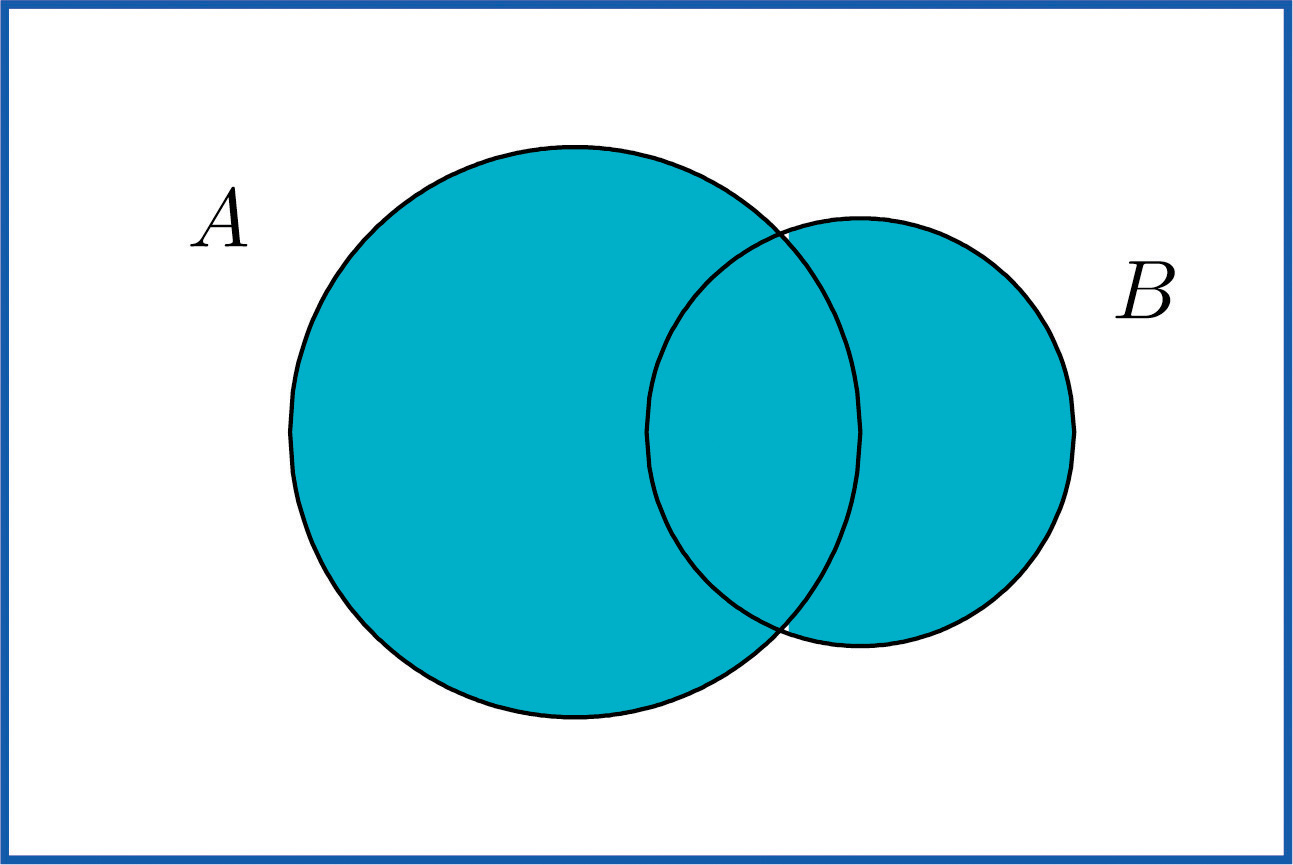
Dire que l'événement A ∪ B s'est produit signifie que lors d'un essai particulier de l'expérience, A ou B s'est produit (ou les deux). Une représentation visuelle de l'union des événements A et B dans un espace échantillon S est donnée dans la Figure 3.5 « L'union des événements » . L'union correspond à la région ombrée.
Figure 3.5 L'union des événements A et B
EXEMPLE 15
Dans l'expérience du lancer d'un seul dé, trouvez l'union des événements E : « le nombre obtenu est pair » et T : « le nombre obtenu est supérieur à deux ».
La solution:
Étant donné que les résultats qui sont dans l'un ou l'autreou(ou les deux) sont 2, 3, 4, 5 et 6,Notez qu'un résultat tel que 4 qui se trouve dans les deux ensembles n'est toujours répertorié qu'une seule fois (bien qu'à proprement parler, il ne soit pas incorrect de le répertorier deux fois).
En mots, l'union est décrite par "le nombre obtenu est pair ou supérieur à deux". Chaque nombre entre un et six sauf le nombre un est pair ou supérieur à deux, correspondant à E ∪ T donné ci-dessus.
EXEMPLE 16
Une famille de deux enfants est sélectionnée au hasard. Soit B l'événement où au moins un enfant est un garçon, soit D l'événement où les sexes des deux enfants diffèrent, et soit M l'événement où les sexes des deux enfants correspondent. Trouver B ∪ D et
La solution:
Un espace échantillon pour cette expérience est, où la première lettre indique le sexe du premier enfant et la deuxième lettre indique le sexe du deuxième enfant. Les événements B , D et M sont
Chaque résultat dans D est déjà dans B , donc les résultats qui sont dans au moins l'un ou l'autre des ensembles B et D ne sont que l'ensemble B lui-même :
Chaque résultat dans l'ensemble de l'espace échantillon S est dans au moins l'un ou l'autre des ensembles B et M , donc
La règle de probabilité additive suivante est une formule utile pour calculer la probabilité de
Règle additive de probabilité
L'exemple suivant, dans lequel nous calculons la probabilité d'une union à la fois en comptant et en utilisant la formule, montre pourquoi le dernier terme de la formule est nécessaire.
EXEMPLE 17
Deux dés équitables sont lancés. Trouvez les probabilités des événements suivants :
- les deux dés montrent un quatre
- au moins un dé montre un quatre
La solution:
Comme ce fut le cas avec le lancement de deux pièces identiques, l'expérience réelle dicte que pour que l'espace échantillon ait des résultats également probables, nous devrions énumérer les résultats comme si nous pouvions distinguer les deux dés. On pourrait imaginer que l'un d'eux est rouge et l'autre vert. Ensuite, tout résultat peut être étiqueté comme une paire de nombres comme dans l'affichage suivant, où le premier nombre de la paire est le nombre de points sur la face supérieure du dé vert et le deuxième nombre de la paire est le nombre de points sur la face supérieure du dé rouge.
- Il y a 36 résultats également probables, dont exactement un correspond à deux quatre, donc la probabilité d'une paire de quatre est de 1/36.
D'après le tableau, nous pouvons voir qu'il y a 11 paires qui correspondent à l'événement en question : les six paires de la quatrième ligne (le dé vert montre un quatre) plus les cinq paires supplémentaires autres que la paire 44, déjà comptée, dans le quatrième colonne (le dé rouge est quatre), donc la réponse est 11/36. Pour voir comment la formule donne le même nombre, supposons que A G désigne l'événement où le dé vert est un quatre et que A R désigne l'événement où le dé rouge est un quatre. Alors clairement en comptant on obtientetDepuis,; c'est le calcul de la partie (a), bien sûr. Ainsi, par la règle additive de probabilité,
EXEMPLE 18
Un service de tutorat se spécialise dans la préparation des adultes aux tests d'équivalence du secondaire. Parmi tous les élèves qui demandent de l'aide au service, 63 % ont besoin d'aide en mathématiques, 34 % ont besoin d'aide en anglais et 27 % ont besoin d'aide en mathématiques et en anglais. Quel est le pourcentage d'élèves qui ont besoin d'aide en mathématiques ou en anglais ?
La solution:
Imaginez que vous sélectionniez un élève au hasard, c'est-à-dire de manière à ce que chaque élève ait la même chance d'être sélectionné. Soit M l'événement « l'élève a besoin d'aide en mathématiques » et soit E l'événement « l'élève a besoin d'aide en anglais ». L'information donnée est que,, etLa règle additive de probabilité donne
Notez comment le raisonnement naïf selon lequel si 63% ont besoin d'aide en mathématiques et 34% ont besoin d'aide en anglais alors 63 plus 34 ou 97% ont besoin d'aide dans l'un ou l'autre donne un nombre trop grand. Le pourcentage qui a besoin d'aide dans les deux matières doit être soustrait, sinon les personnes ayant besoin d'aide dans les deux matières sont comptées deux fois, une fois pour avoir besoin d'aide en mathématiques et une fois pour avoir besoin d'aide en anglais. La simple somme des probabilités fonctionnerait si les événements en question s'excluaient mutuellement, car alorsest nul et ne fait aucune différence.
EXEMPLE 19
Les volontaires pour un effort de secours en cas de catastrophe ont été classés selon leur spécialité ( C : construction, E : éducation, M : médecine) et leur capacité linguistique ( S : parle couramment une seule langue, T : parle couramment deux langues ou plus). Les résultats sont présentés dans le tableau de classification à double entrée suivant :
| Spécialité | La capacité de la langue | |
|---|---|---|
| S | J | |
| C | 12 | 1 |
| E | 4 | 3 |
| M | 6 | 2 |
La première rangée de chiffres signifie que 12 bénévoles dont la spécialité est la construction parlent couramment une seule langue, et 1 bénévole dont la spécialité est la construction parle couramment au moins deux langues. De même pour les deux autres lignes.
Un volontaire est choisi au hasard, c'est-à-dire que chacun a une chance égale d'être choisi. Trouvez la probabilité que :
- sa spécialité est la médecine et il parle deux langues ou plus ;
- soit sa spécialité est la médecine, soit il parle deux langues ou plus ;
- sa spécialité est autre chose que la médecine.
La solution:
Lorsque les informations sont présentées dans un tableau de classification à double entrée, il est généralement pratique de joindre au tableau les totaux des lignes et des colonnes, pour produire un nouveau tableau comme celui-ci :
| Spécialité | La capacité de la langue | Total | |
|---|---|---|---|
| S | J | ||
| C | 12 | 1 | 13 |
| E | 4 | 3 | sept |
| M | 6 | 2 | 8 |
| Total | 22 | 6 | 28 |
- La probabilité recherchée estLe tableau montre qu'il y a 2 de ces personnes, sur 28 en tout, d'oùsoit environ 7 % de chances.
La probabilité recherchée estLe total de la troisième ligne et le total général de l'échantillon donnentLe total de la deuxième colonne et le total général donnentAinsi, en utilisant le résultat de la partie (a),
soit environ 43 % de chances.
Cette probabilité peut être calculée de deux manières. Étant donné que l'événement d'intérêt peut être considéré comme l'événement C ∪ E et que les événements C et E s'excluent mutuellement, la réponse est, en utilisant les totaux des deux premières lignes,
D'autre part, l'événement d'intérêt peut être considéré comme le complément M c de M , donc en utilisant la valeur decalculé dans la partie (b),
comme avant.
CLÉ À EMPORTER
- La probabilité d'un événement qui est un complément ou une union d'événements de probabilité connue peut être calculée à l'aide de formules.
DES EXERCICES
Pour l'espace échantillonidentifier le complément de chaque événement donné.
- S
Pour l'espace échantillonidentifier le complément de chaque événement donné.
- ∅ (l'ensemble "vide" qui n'a pas d'éléments)
L'espace d'échantillonnage pour trois lancers de pièce est
Définir des événements
- Énumérez les résultats qui comprennent H et M .
- Énumérez les résultats qui comprennent H ∩ M , H ∪ M et H c .
- En supposant que tous les résultats sont également probables, trouvez,, et
- Déterminez si H c et M s'excluent mutuellement ou non. expliquez pourquoi ou pourquoi pas.
Pour l'expérience consistant à lancer un seul dé à six faces une fois, définissez les événements
- Énumérez les résultats qui comprennent T et G .
- Énumérez les résultats qui comprennent T ∩ G , T ∪ G , T c , et
- En supposant que tous les résultats sont également probables, trouvez,, et
- Déterminez si T et G sont mutuellement exclusifs ou non. expliquez pourquoi ou pourquoi pas.
Un jeu spécial de 16 cartes en contient 4 bleues, 4 jaunes, 4 vertes et 4 rouges. Les quatre cartes de chaque couleur sont numérotées de un à quatre. Une seule carte est tirée au hasard. Définir des événements
- Énumérez les résultats qui comprennent B , R et N .
- Énumérez les résultats qui comprennent B ∩ R , B ∪ R , B ∩ N , R ∪ N , B c , et
- En supposant que tous les résultats sont également probables, trouvez les probabilités des événements dans la partie précédente.
- Déterminez si B et N sont mutuellement exclusifs ou non. expliquez pourquoi ou pourquoi pas.
Dans le cadre du problème précédent, définir des événements
- Énumérez les résultats qui comprennent Y , I et J .
- Énumérez les résultats qui comprennent Y ∩ I , Y ∪ J , I ∩ J , I c et
- En supposant que tous les résultats sont également probables, trouvez les probabilités des événements dans la partie précédente.
- Déterminez si I c et J s'excluent mutuellement ou non. expliquez pourquoi ou pourquoi pas.
Le diagramme de Venn fourni montre un espace échantillon et deux événements A et B . Supposer,,,, etConfirmez que les probabilités des résultats totalisent 1, puis calculez les probabilités suivantes.
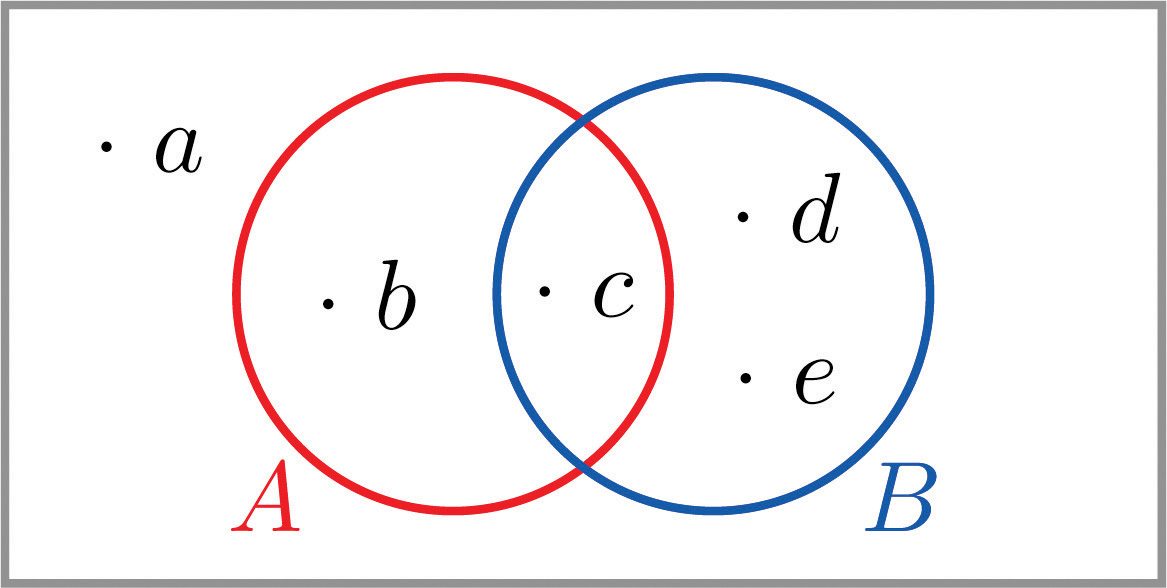
- deux façons : (i) en trouvant les résultats dans A c et en ajoutant leurs probabilités, et (ii) en utilisant la règle de probabilité pour les compléments.
- deux façons : (i) en trouvant les résultats dans A ∪ B et en ajoutant leurs probabilités, et (ii) en utilisant la règle additive de probabilité.
Le diagramme de Venn fourni montre un espace échantillon et deux événements A et B . Supposer,,, etConfirmez que les probabilités des résultats totalisent 1, puis calculez les probabilités suivantes.
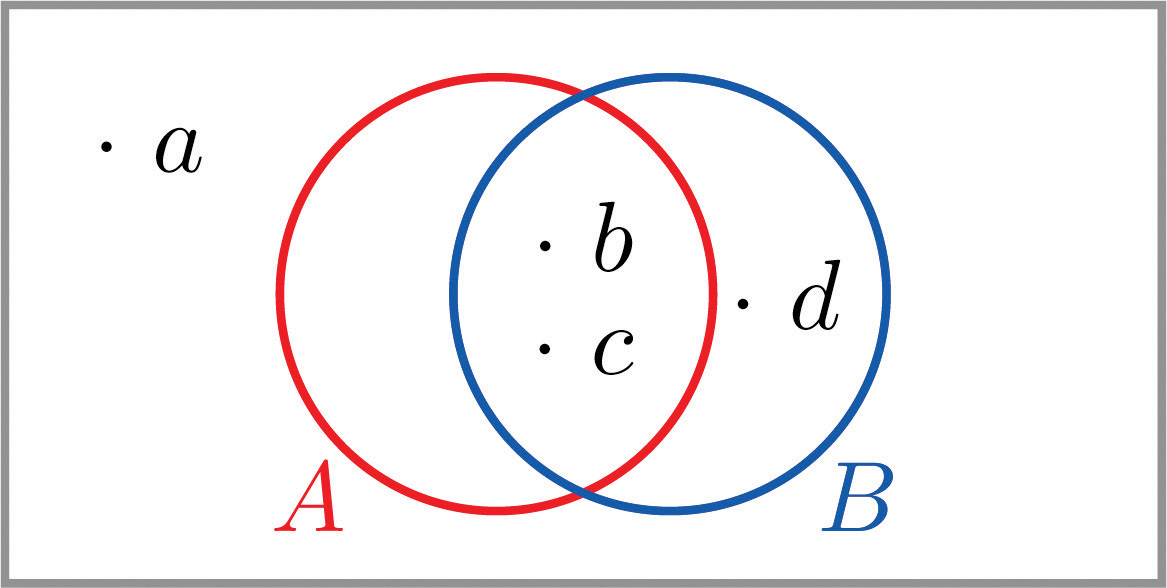
- deux façons : (i) en trouvant les résultats dans A c et en ajoutant leurs probabilités, et (ii) en utilisant la règle de probabilité pour les compléments.
- deux façons : (i) en trouvant les résultats dans A ∪ B et en ajoutant leurs probabilités, et (ii) en utilisant la règle additive de probabilité.
Confirmez que les probabilités du tableau de contingence à deux facteurs totalisent 1, puis utilisez-le pour trouver les probabilités des événements indiqués.
tu V O UN 0,15 0,00 0,23 B 0,22 0,30 0,10 - ,,
- ,,
- Déterminer si oui ou non les événements A et U sont mutuellement exclusifs ; les événements A et V .
Confirmez que les probabilités du tableau de contingence à deux facteurs totalisent 1, puis utilisez-le pour trouver les probabilités des événements indiqués.
R S J M 0,09 0,25 0,19 N 0,31 0,16 0,00 - ,,
- ,,
- Déterminer si les événements N et S s'excluent mutuellement ou non ; les événements N et T .
DE BASE
Faites une déclaration en anglais ordinaire qui décrit le complément de chaque événement (ne vous contentez pas d'insérer le mot « not »).
- Au lancer de dé : « cinq ou plus ».
- Dans un lancer de dé : « un nombre pair ».
- En deux lancers de pièce : « au moins un face ».
- Dans la sélection aléatoire d'un étudiant: "Pas un étudiant de première année."
Faites une déclaration en anglais ordinaire qui décrit le complément de chaque événement (ne vous contentez pas d'insérer le mot « not »).
- Au lancer de dé : « deux ou moins ».
- Au lancer de dé : « un, trois ou quatre ».
- En deux lancers de pièce : « au plus un face ».
- Dans la sélection aléatoire d'un étudiant: "Ni un étudiant de première année ni un senior."
L'espace d'échantillonnage qui décrit toutes les familles de trois enfants selon le sexe des enfants par rapport au rang de naissance est
Pour chacun des événements suivants dans l'expérience de sélection aléatoire d'une famille de trois enfants, indiquez le complément de l'événement dans les termes les plus simples possibles, puis trouvez les résultats qui composent l'événement et son complément.
- Au moins un enfant est une fille.
- Au plus un enfant est une fille.
- Tous les enfants sont des filles.
- Exactement deux des enfants sont des filles.
- Le premier né est une fille.
L'espace d'échantillonnage qui décrit la classification bidirectionnelle des citoyens selon le sexe et l'opinion sur une question politique est
où la première lettre désigne le sexe ( m : masculin, f : féminin) et la seconde opinion ( f : pour, a : contre, n : neutre). Pour chacun des événements suivants dans l'expérience de sélection aléatoire d'un citoyen, indiquez le complément de l'événement dans les termes les plus simples possibles, puis trouvez les résultats qui composent l'événement et son complément.
- La personne est de sexe masculin.
- La personne n'est pas favorable.
- La personne est soit masculine, soit favorable.
- La personne est féminine et neutre.
Un touriste qui parle anglais et allemand mais aucune autre langue visite une région de Slovénie. Si 35% des habitants parlent anglais, 15% parlent allemand et 3% parlent à la fois anglais et allemand, quelle est la probabilité que le touriste puisse parler avec un habitant de la région rencontré au hasard ?
Dans un certain pays, 43 % de toutes les automobiles sont équipées d'airbags, 27 % ont des freins antiblocage et 13 % ont les deux. Quelle est la probabilité qu'un véhicule sélectionné au hasard ait à la fois des airbags et des freins antiblocage ?
Un fabricant examine ses dossiers au cours de la dernière année sur un composant reçu de fournisseurs extérieurs. La répartition par source (fournisseur A , fournisseur B ) et qualité ( H : élevée, U : utilisable, D : défectueuse) est présentée dans le tableau de contingence à double entrée.
H tu ré UN 0,6937 0,0049 0,0014 B 0,2982 0,0009 0,0009 L'enregistrement d'une partie est sélectionné au hasard. Trouvez la probabilité de chacun des événements suivants.
- La pièce était défectueuse.
- La partie était soit de haute qualité, soit au moins utilisable, de deux manières : (i) en ajoutant des nombres dans le tableau, et (ii) en utilisant la réponse à (a) et la règle de probabilité pour les compléments.
- La pièce était défectueuse et provenait du fournisseur B .
- La pièce était défectueuse ou provenait du fournisseur B , de deux manières : en trouvant dans le tableau les cellules correspondant à cet événement et en additionnant leurs probabilités, et (ii) en utilisant la règle additive de probabilité.
Les personnes atteintes d'une condition médicale particulière ont été classées en fonction de la présence ( T ) ou de l'absence ( N ) d'une toxine potentielle dans leur sang et de l'apparition de la condition ( E : précoce, M : moyen, L : tardif). La répartition selon cette classification est présentée dans le tableau de contingence à double entrée.
E M L J 0,012 0,124 0,013 N 0,170 0,638 0,043 L'un de ces individus est tiré au sort. Trouvez la probabilité de chacun des événements suivants.
- La personne a connu un début précoce de la maladie.
- L'apparition de la condition était soit moyenne, soit tardive, de deux manières : (i) en ajoutant des nombres dans le tableau, et (ii) en utilisant la réponse à (a) et la règle de probabilité pour les compléments.
- La toxine est présente dans le sang de la personne.
- La personne a connu l'apparition précoce de la maladie et la toxine est présente dans le sang de la personne.
- La personne a connu un début précoce de la maladie ou la toxine est présente dans le sang de la personne, de deux manières : (i) en trouvant les cellules du tableau qui correspondent à cet événement et en ajoutant leurs probabilités, et (ii) en utilisant la règle additive de probabilité.
La répartition des étudiants inscrits dans un cursus universitaire par promotion ( F : première année,: deuxième année, J : junior,: senior) et majeure académique ( S : sciences, mathématiques ou ingénierie, L : arts libéraux, O : autre) est indiquée dans le tableau de classification à double entrée.
Principal Classer F Alors J Se S 92 42 20 13 L 368 167 80 53 O 460 209 100 67 Un étudiant inscrit au cours est tiré au sort. Joignez les totaux des lignes et des colonnes au tableau et utilisez le tableau développé pour trouver la probabilité de chacun des événements suivants.
- L'étudiant est un étudiant de première année.
- L'étudiant est une majeure en arts libéraux.
- L'étudiant est un étudiant de première année en arts libéraux.
- L'étudiant est soit un étudiant de première année, soit un étudiant en arts libéraux.
- L'étudiant n'est pas une majeure en arts libéraux.
Le tableau relie la réponse à un appel de fonds par un collège à ses anciens élèves au nombre d'années écoulées depuis l'obtention du diplôme.
Réponse Années depuis l'obtention du diplôme 0–5 6–20 21–35 Plus de 35 Positif 120 440 210 90 Aucun 1380 3560 3290 910 Un diplômé est tiré au sort. Joignez les totaux des lignes et des colonnes au tableau et utilisez le tableau développé pour trouver la probabilité de chacun des événements suivants.
- L'ancien a répondu.
- L'ancien n'a pas répondu.
- L'ancien élève a obtenu son diplôme il y a au moins 21 ans.
- L'ancien élève a obtenu son diplôme il y a au moins 21 ans et a répondu.
APPLICATIONS
L'espace d'échantillonnage pour lancer trois pièces est
- Énumérez les résultats qui correspondent à l'énoncé « Toutes les pièces sont des faces ».
- Énumérez les résultats qui correspondent à l'énoncé « Toutes les pièces ne sont pas des faces ».
- Énumérez les résultats qui correspondent à l'énoncé « Toutes les pièces ne sont pas des faces ».
EXERCICES SUPPLÉMENTAIRES
RÉPONSES
- ∅
- ,
- ,,
- ,,
- S'excluent mutuellement parce qu'ils n'ont aucun élément en commun.
- ,,
- , ,
- ,,,,,
- Ne s'excluent pas mutuellement car ils ont un élément en commun.
- 0,36
- 0,78
- 0,64
- 0,27
- 0,87
- ,,
- ,,
- 0,7
- 0,7
- A et U ne sont pas mutuellement exclusifs carest le nombre non nul 0,15. A et V s'excluent mutuellement car
- "quatre ou moins"
- "un nombre impair"
- "sans pile" ou "tout pile"
- "un étudiant de première année"
"Tous les enfants sont des garçons."
Événement:,
Complément:
« Au moins deux des enfants sont des filles » ou « Il y a deux ou trois filles ».
Événement:,
Complément:
"Au moins un enfant est un garçon."
Événement:,
Complément:
« Soit il n'y a pas de filles, soit exactement une fille, soit trois filles.
Événement:,
Complément:
"Le premier-né est un garçon."
Événement:,
Complément:
0,47
- 0,0023
- 0,9977
- 0,0009
- 0,3014
- 920/1671
- 668/1671
- 368/1671
- 1220/1671
- 1003/1671
3.3 Probabilité conditionnelle et événements indépendants
OBJECTIFS D'APPRENTISSAGE
- Apprendre le concept d'une probabilité conditionnelle et comment la calculer.
- Apprendre le concept d'indépendance des événements et comment l'appliquer.
Probabilite conditionnelle
Supposons qu'un dé équitable ait été lancé et qu'on vous demande de donner la probabilité qu'il s'agisse d'un cinq. Il y a six résultats également probables, donc votre réponse est 1/6. Mais supposons qu'avant de donner votre réponse, vous receviez l'information supplémentaire que le nombre obtenu était impair. Puisqu'il n'y a que trois nombres impairs possibles, dont l'un est cinq, vous réviserez certainement votre estimation de la probabilité qu'un cinq soit obtenu de 1/6 à 1/3. En général, la probabilité révisée qu'un événement A se soit produit, en tenant compte de l'information supplémentaire qu'un autre événement B s'est définitivement produit lors de cet essai de l'expérience, est appelée la probabilité conditionnelle de A étant donné Bet est noté parLe raisonnement utilisé dans cet exemple peut être généralisé pour donner la formule de calcul dans la définition suivante.
Définition
La probabilité conditionnelle de A étant donné B , notée , est la probabilité que l'événement A se soit produit dans un essai d'une expérience aléatoire pour laquelle on sait que l'événement B s'est définitivement produit. Il peut être calculé au moyen de la formule suivante :
Règle de probabilité conditionnelle
EXEMPLE 20
Un dé juste est lancé.
- Trouvez la probabilité que le nombre obtenu soit un cinq, étant donné qu'il est impair.
- Trouvez la probabilité que le nombre obtenu soit impair, étant donné qu'il s'agit d'un cinq.
La solution:
L'espace d'échantillonnage pour cette expérience est l'ensemblecomposé de six résultats également probables. Soit F l'événement « un cinq est lancé » et soit O l'événement « un nombre impair est lancé », de sorte que
Ceci est l'exemple d'introduction, nous savons donc déjà que la réponse est 1/3. Pour utiliser la formule dans la définition pour confirmer cela, nous devons remplacer A dans la formule (l'événement dont nous cherchons à estimer la probabilité) par F et remplacer B (l'événement dont nous savons avec certitude qu'il s'est produit) par O :
Depuis,
Depuis,
Ainsi
C'est le même problème, mais avec les rôles de F et O inversés. Puisqu'on nous donne que le nombre qui a été lancé est cinq, ce qui est impair, la probabilité en question doit être 1. Pour appliquer la formule à ce cas, nous devons maintenant remplacer A (l'événement dont nous cherchons à estimer la probabilité) par O et B (l'événement dont nous savons avec certitude qu'il s'est produit) par F :
ÉvidemmentDans la partie (a), nous avons constaté queAinsi
Tout comme nous n'avions pas besoin de la formule de calcul dans cet exemple, nous n'en avons pas besoin lorsque les informations sont présentées dans un tableau de classification à double entrée, comme dans l'exemple suivant.
EXEMPLE 21
Dans un échantillon de 902 individus de moins de 40 ans mariés ou ayant été mariés, chacun a été classé selon son sexe et son âge au premier mariage. Les résultats sont résumés dans le tableau de classification à double entrée suivant, où la signification des étiquettes est :
- M : mâle
- F : femelle
- E : adolescent lors du premier mariage
- W : dans la vingtaine au moment du premier mariage
- H : dans la trentaine au premier mariage
| E | O | H | Total | |
|---|---|---|---|---|
| M | 43 | 293 | 114 | 450 |
| F | 82 | 299 | 71 | 452 |
| Total | 125 | 592 | 185 | 902 |
Les chiffres de la première ligne signifient que 43 personnes de l'échantillon étaient des hommes qui se sont mariés pour la première fois à l'adolescence, 293 étaient des hommes qui se sont mariés pour la première fois dans la vingtaine, 114 hommes qui se sont mariés pour la première fois dans la trentaine et un total de 450 personnes. dans l'échantillon étaient des hommes. De même pour les nombres de la deuxième ligne. Les chiffres de la dernière ligne signifient que, quel que soit leur sexe, 125 personnes de l'échantillon étaient mariées à l'adolescence, 592 dans la vingtaine, 185 dans la trentaine, et qu'il y avait au total 902 personnes dans l'échantillon. Supposons que les proportions dans l'échantillon reflètent fidèlement celles de la population de tous les individus de la population qui ont moins de 40 ans et qui sont ou ont été mariés. Supposons qu'une telle personne soit choisie au hasard.
- Trouvez la probabilité que l'individu sélectionné soit un adolescent au premier mariage.
- Trouvez la probabilité que l'individu sélectionné ait été un adolescent au premier mariage, étant donné qu'il s'agit d'un homme.
La solution:
Il est naturel de laisser E désigner également l'événement selon lequel la personne sélectionnée était adolescente au premier mariage et de laisser M désigner l'événement selon lequel la personne sélectionnée est un homme.
- Selon le tableau, la proportion d'individus de l'échantillon qui étaient adolescents lors de leur premier mariage est de 125/902. Il s'agit de la fréquence relative de ces personnes dans la population, d'oùsoit environ 14 %.
Puisqu'il est connu que la personne sélectionnée est un homme, toutes les femmes peuvent être supprimées, de sorte que seule la ligne du tableau correspondant aux hommes de l'échantillon s'applique :
E O H Total M 43 293 114 450
La proportion d'hommes de l'échantillon qui étaient adolescents lors de leur premier mariage est de 43/450. Il s'agit de la fréquence relative de ces personnes dans la population masculine, d'oùsoit environ 10 %.
Dans l'exemple suivant, la formule de calcul de la définition doit être utilisée.
EXEMPLE 22
Supposons que dans une population adulte, la proportion de personnes à la fois en surpoids et souffrant d'hypertension soit de 0,09 ; la proportion de personnes qui ne sont pas en surpoids mais qui souffrent d'hypertension est de 0,11 ; la proportion de personnes en surpoids mais ne souffrant pas d'hypertension est de 0,02 ; et la proportion de personnes qui ne sont ni en surpoids ni souffrant d'hypertension est de 0,78. Un adulte est choisi au hasard dans cette population.
- Trouver la probabilité que la personne sélectionnée souffre d'hypertension étant donné qu'elle est en surpoids.
- Trouver la probabilité que la personne sélectionnée souffre d'hypertension étant donné qu'elle n'est pas en surpoids.
- Comparez les deux probabilités que vous venez de trouver pour répondre à la question de savoir si les personnes en surpoids ont tendance à souffrir d'hypertension.
La solution:
Soit H l'événement "la personne sélectionnée souffre d'hypertension". Soit O l'événement "la personne sélectionnée est en surpoids". Les informations de probabilité données dans le problème peuvent être organisées dans le tableau de contingence suivant :
| O | O c | |
|---|---|---|
| H | 0,09 | 0,11 |
| H c | 0,02 | 0,78 |
En utilisant la formule dans la définition de la probabilité conditionnelle,
En utilisant la formule dans la définition de la probabilité conditionnelle,
- est plus de six fois plus grand que, ce qui indique un taux d'hypertension beaucoup plus élevé chez les personnes en surpoids que chez les personnes sans surpoids. Il pourrait être intéressant de noter qu'une comparaison directe deetne répond pas à la même question.
Événements indépendants
Bien que nous attendions généralement la probabilité conditionnelleêtre différent de la probabilitéde A , il n'est pas nécessaire qu'il soit différent deLorsque, l'occurrence de B n'a aucun effet sur la probabilité de A . Que l'événement A se soit produit ou non est indépendant de l'événement B .
En utilisant l'algèbre, on peut montrer que l'égalitévaut si et seulement si l'égalitéest vrai, ce qui est vrai si et seulement siC'est la base de la définition suivante.
Définition
Les événements A et B sont indépendants si
Si A et B ne sont pas indépendants alors ils sont dépendants .
La formule de la définition a deux utilisations pratiques mais exactement opposées :
Dans une situation où nous pouvons calculer les trois probabilités,, et, il permet de vérifier si les événements A et B sont indépendants ou non :
- Si, alors A et B sont indépendants.
- Si, alors A et B ne sont pas indépendants.
- Dans une situation où chacun deetpeut être calculé et on sait que A et B sont indépendants, alors on peut calculeren multipliant ensembleet:
EXEMPLE 23
Un seul dé équitable est lancé. LaisseretA et B sont - ils indépendants ?
La solution:
Dans cet exemple, nous pouvons calculer les trois probabilités,, etDepuis le produitn'est pas le même nombre que, les événements A et B ne sont pas indépendants.
EXEMPLE 24
La classification à double entrée des adultes mariés ou précédemment mariés de moins de 40 ans selon le sexe et l'âge au premier mariage dans la note 3.48 "Exemple 21" a produit le tableau
| E | O | H | Total | |
|---|---|---|---|---|
| M | 43 | 293 | 114 | 450 |
| F | 82 | 299 | 71 | 452 |
| Total | 125 | 592 | 185 | 902 |
Déterminez si les événements F : « féminin » et E : « était adolescente au premier mariage » sont indépendants ou non.
La solution:
Le tableau montre que dans l'échantillon de 902 de ces adultes, 452 étaient des femmes, 125 étaient des adolescentes lors de leur premier mariage et 82 étaient des femmes adolescentes lors de leur premier mariage, de sorte que
Depuis
n'est pas le même que
nous concluons que les deux événements ne sont pas indépendants.
EXEMPLE 25
De nombreux tests de diagnostic pour détecter des maladies ne testent pas directement la maladie, mais un produit chimique ou biologique de la maladie, et ne sont donc pas parfaitement fiables. La sensibilité d'un test est la probabilité que le test soit positif lorsqu'il est administré à une personne atteinte de la maladie. Plus la sensibilité est élevée, plus le taux de détection est élevé et plus le taux de faux négatifs est faible.
Supposons que la sensibilité d'une procédure de diagnostic pour tester si une personne a une maladie particulière est de 92 %. Une personne réellement atteinte de la maladie est testée selon cette procédure par deux laboratoires indépendants.
- Quelle est la probabilité que les résultats des deux tests soient positifs ?
- Quelle est la probabilité qu'au moins un des deux résultats du test soit positif ?
La solution:
Soit A 1 l'événement « le test du premier laboratoire est positif » et soit A 2 l'événement « le test du second laboratoire est positif ». Comme A 1 et A 2 sont indépendants,
En utilisant la règle additive de probabilité et la probabilité qui vient d'être calculée,
EXEMPLE 26
La spécificité d'un test de diagnostic d'une maladie est la probabilité que le test soit négatif lorsqu'il est administré à une personne qui n'a pas la maladie. Plus la spécificité est élevée, plus le taux de faux positifs est faible.
Supposons que la spécificité d'une procédure de diagnostic pour tester si une personne a une maladie particulière est de 89 %.
- Une personne qui n'a pas la maladie est testée à l'aide de cette procédure. Quelle est la probabilité que le résultat du test soit positif ?
- Une personne qui n'a pas la maladie est testée par deux laboratoires indépendants utilisant cette procédure. Quelle est la probabilité que les résultats des deux tests soient positifs ?
La solution:
Soit B l'événement "le résultat du test est positif". Le complément de B est que le résultat du test est négatif et a une probabilité de spécificité du test de 0,89. Ainsi
Soit B 1 l'événement « le test du premier laboratoire est positif » et B 2 l'événement « le test du second laboratoire est positif ». Comme B 1 et B 2 sont indépendants, d'après la partie (a) de l'exemple
Le concept d'indépendance s'applique à un certain nombre d'événements. Par exemple, trois événements A , B et C sont indépendants siNotez bien que, comme c'est le cas avec seulement deux événements, ce n'est pas une formule qui est toujours valable, mais vaut précisément lorsque les événements en question sont indépendants.
EXEMPLE 27
La fiabilité d'un système peut être améliorée par la redondance, ce qui signifie la construction de deux dispositifs indépendants ou plus pour faire le même travail, comme deux systèmes de freinage indépendants dans une automobile.
Supposons qu'une espèce particulière de chiens dressés ait 90 % de chances de détecter de la contrebande dans les bagages des compagnies aériennes. Si les bagages sont contrôlés trois fois par trois chiens différents indépendamment les uns des autres, quelle est la probabilité que la contrebande soit détectée ?
La solution:
Soit D 1 l'événement où la contrebande est détectée par le premier chien, D 2 l'événement où elle est détectée par le deuxième chien, et D 3 l'événement où elle est détectée par le troisième. Étant donné que chaque chien a 90% de détection de la contrebande, selon la règle de probabilité pour les compléments, il a 10% de chances d'échouer. En symboles, , et
Soit D l'événement où la contrebande est détectée. Nous cherchonsC'est plus facile à trouver, car bien qu'il y ait plusieurs façons de détecter la contrebande, il n'y a qu'une seule façon de passer inaperçue : les trois chiens doivent échouer. Ainsi, et
Mais les événements D 1 , D 2 et D 3 sont indépendants, ce qui implique que leurs complémentaires sont indépendants, donc
En utilisant ce nombre dans l'affichage précédent, nous obtenons
Autrement dit, bien qu'un chien n'ait que 90 % de chances de détecter la contrebande, trois chiens travaillant indépendamment ont 99,9 % de chances de le détecter.
Probabilités sur les diagrammes en arbre
Certains problèmes de probabilité sont rendus beaucoup plus simples lorsqu'ils sont abordés à l'aide d'un diagramme en arbre. L'exemple suivant illustre comment placer des probabilités sur un diagramme en arbre et l'utiliser pour résoudre un problème.
EXEMPLE 28
Un bocal contient 10 billes, 7 noires et 3 blanches. Deux billes sont tirées sans remise, c'est-à-dire que la première n'est pas remise en place avant que la seconde ne soit tirée.
- Quelle est la probabilité que les deux billes soient noires ?
- Quelle est la probabilité qu'exactement une bille soit noire ?
- Quelle est la probabilité qu'au moins une bille soit noire ?
La solution:
Un diagramme en arbre pour la situation de dessiner une bille après l'autre sans remplacement est montré dans la Figure 3.6 "Schéma en arbre pour dessiner deux billes" . Le cercle et le rectangle seront expliqués plus tard et doivent être ignorés pour le moment.
Illustration 3.6Diagramme en arbre pour dessiner deux billes
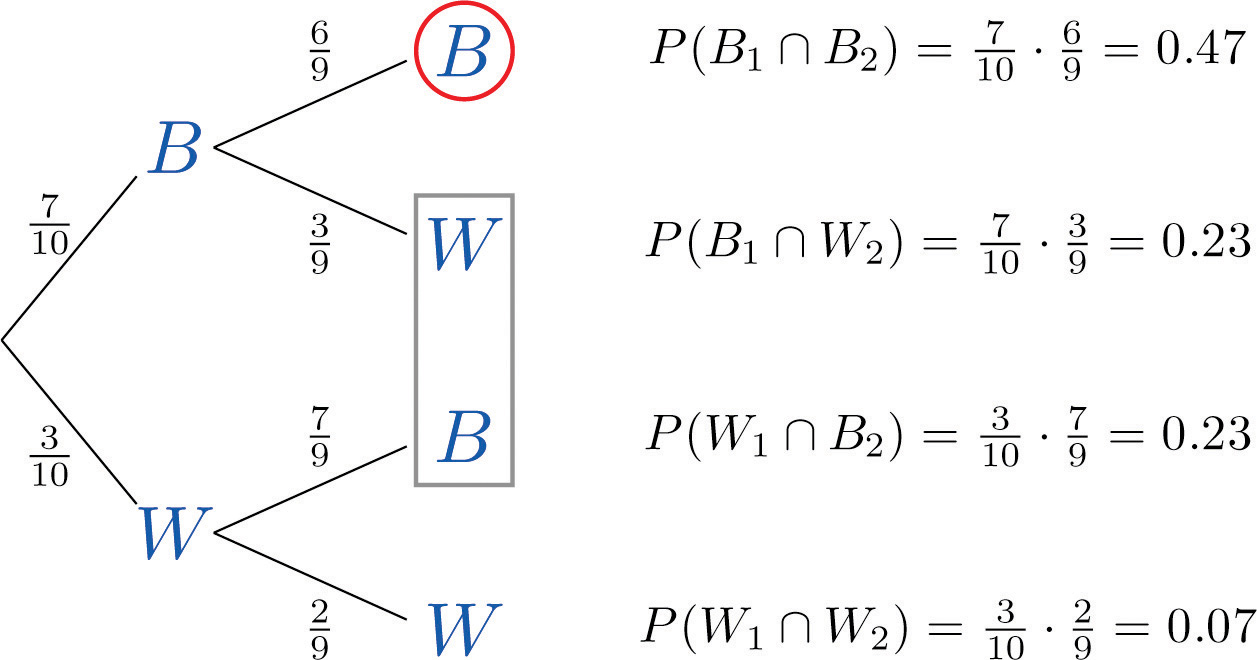
Les chiffres sur les deux branches les plus à gauche sont les probabilités d'obtenir soit une bille noire, 7 sur 10, soit une bille blanche, 3 sur 10, au premier tirage. Le nombre sur chaque branche restante est la probabilité que l'événement correspondant au nœud à l'extrémité droite de la branche se produise, étant donné que l'événement correspondant au nœud à l'extrémité gauche de la branche s'est produit. Ainsi pour la branche supérieure, reliant les deux B, il est, où B 1 désigne l'événement « la première bille tirée est noire » et B 2 désigne l'événement « la deuxième bille tirée est noire ». Puisqu'après avoir tiré une bille noire il reste 9 billes dont 6 noires, cette probabilité est de 6/9.
Le nombre à droite de chaque nœud final est calculé comme indiqué, en utilisant le principe que si la formule de la règle conditionnelle de probabilité est multipliée par, alors le résultat est
- L'événement "les deux billes sont noires" estet correspond au nœud supérieur droit de l'arbre, qui a été encerclé. Ainsi, comme indiqué ici, il est de 0,47.
- L'événement "exactement une bille est noire" correspond aux deux nœuds de l'arbre entourés par le rectangle. Les événements qui correspondent à ces deux nœuds s'excluent mutuellement : noir suivi de blanc est incompatible avec blanc suivi de noir. Ainsi, conformément à la règle additive de probabilité, nous ajoutons simplement les deux probabilités à côté de ces nœuds, car ce qui serait soustrait de la somme est zéro. Ainsi la probabilité de tirer exactement une bille noire en deux essais est
L'événement « au moins une bille est noire » correspond aux trois nœuds de l'arbre entourés soit par le cercle, soit par le rectangle. Les événements qui correspondent à ces nœuds sont mutuellement exclusifs, de sorte que dans la partie (b) nous ajoutons simplement les probabilités à côté de ces nœuds. Ainsi la probabilité de tirer au moins une bille noire en deux essais est
Bien sûr, cette réponse aurait pu être trouvée plus facilement en utilisant la loi de probabilité des compléments, en soustrayant simplement la probabilité de l'événement complémentaire, "deux billes blanches sont tirées", de 1 pour obtenir
Comme le montre cet exemple, trouver la probabilité pour chaque branche est assez simple, puisque nous la calculons en sachant tout ce qui s'est passé dans la séquence d'étapes jusqu'à présent. Deux principes vrais en général se dégagent de cet exemple :
Probabilités sur les diagrammes en arbre
- La probabilité de l'événement correspondant à n'importe quel nœud d'un arbre est le produit des nombres sur le chemin unique de branches qui mène à ce nœud depuis le début.
- Si un événement correspond à plusieurs nœuds finaux, alors sa probabilité est obtenue en additionnant les nombres à côté de ces nœuds.
POINTS CLÉS À RETENIR
- Une probabilité conditionnelle est la probabilité qu'un événement se soit produit, en tenant compte d'informations supplémentaires sur le résultat de l'expérience.
- Une probabilité conditionnelle peut toujours être calculée à l'aide de la formule de la définition. Parfois, il peut être calculé en supprimant une partie de l'espace échantillon.
- Deux événements A et B sont indépendants si la probabilitéde leur intersection A ∩ B est égal au produitde leurs probabilités individuelles.


